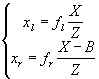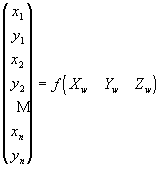1. Sistemi di visione:
    Visione Tridimensionale nei Processi di Produzione - "Stato dell’Arte"
    Michele Lanzetta
    Dott. Ing. Michele Lanzetta - Dottore di Ricerca in Automazione e Robotica Industriale - DIP - Dipartimento di Ingegneria della Produzione - Università degli Studi di Pisa - E-mail: m.lanzetta@ing.unipi.it

    2. Rassegna di applicazioni della visione 3-D in campo industriale. Classificazione in funzione del tipo di impiego, della configurazione adottata e degli algoritmi implementati. Descrizione dei metodi di calibrazione e dei principali approcci con riferimenti alla letteratura scientifica recente.

    1. Introduzione

      2. La visione 3-D (tridimensionale) rappresenta attualmente l’ultima frontiera della ricerca sia a livello di creazione di modelli del problema per la definizione di algoritmi affidabili ed efficienti, sia a livello hardware per le spiccate esigenze di potenza di calcolo.

      In campo bidimensionale è stata già maturata a partire dagli anni ’70, in cui la visione ha iniziato a diffondersi, una vasta esperienza che consente la produzione di hardware special purpose per applicazioni in linea di produzione basato su algoritmi consolidati, caratterizzato da bassi costi e facilità di programmazione.

      La visione tridimensionale interessa una vasta tipologia di applicazioni industriali.

      Gran parte delle applicazioni più avanzate in campo tridimensionale appartengono alla robotica [], [], [], [] dal momento che il senso della vista fornisce, anche ad un robot oltre che all’uomo, la stragrande maggioranza di informazioni necessarie per la navigazione [], [], [] per evitare ostacoli [] e per l’interazione con il mondo esterno. Tuttavia le medesime esigenze riguardano sempre più il campo industriale data la crescente diffusione di automazione flessibile e la disponibilità di hardware (processori, memorie, ecc.) a costi competitivi.

      Esistono applicazioni della visione tridimensionale anche in campi diversi da quello industriale, come nella guida di autoveicoli [], [], [], [], [].

      Gli algoritmi sono basati in misura crescente non più esclusivamente sulla logica tradizionale, cioè su sistemi del tipo IF-THEN-ELSE con albero delle decisioni, ma anche su logica sfumata (fuzzy) o su sistemi di classificazione di tipo neurale (o neuronale) [], su sistemi esperti (knowledge-based) [] o su altre tecniche che fanno parte della cosiddetta AI (Intelligenza Artificiale, Artificial Intelligence) [].

      In questo articolo verrà indicata una possibile schematizzazione delle potenzialità della visione artificiale tridimensionale in campo industriale con una rassegna di alcuni tra i più significativi esempi presenti in letteratura (capitolo 2). Verranno inoltre indicate le possibili configurazioni con i metodi di calibrazione (capitolo 3) e la descrizione dei principali approcci (capitolo 4) [].

      Nella parte II [], vengono proposti due algoritmi. Il primo, basato su primitive geometriche, per determinare la posizione 3-D di oggetti osservati con un sistema di visione di tipo neurale a singola telecamera attraverso l’estrazione di archi ellittici dai contorni. Il secondo rappresenta un approccio innovativo al problema del match e consente di ricostruire qualsiasi scena osservata da un sistema stereoscopico di cui è stata eseguita la calibrazione.

    2. Applicazioni industriali della visione tridimensionale

Facendo riferimento ad un sistema di classificazione consolidato, le tecnologie possono essere suddivise nelle seguenti famiglie []:

  1. montaggio [], [], [], [], [], smontaggio ad esempio a scopo di riciclaggio, trattato nel paragrafo 2.A;

  2. taglio o asportazione di truciolo, ad esempio con macchine utensili a controllo numerico, trattato nel paragrafo 2. F;

  3. processi elettrofisici e elettrochimici, ad esempio, saldatura, rapid prototyping;

  4. processi abrasivi, ad esempio rettifica, idrotaglio (water-jet);

  5. formatura a freddo e a caldo, ad esempio stampaggio;

  6. progettazione con tecniche CAD (Computer Aided Design), trattata nel paragrafo 2.E;

  7. metrologia [], trattata nel paragrafo 2.D;

  8. superfici [], [].

Riguardo al processo produttivo il sistema di visione può essere impiegato in tutte le fasi:

  1. nel controllo della materia prima;

  2. durante la lavorazione di pezzi;

  3. nell’assemblaggio, ad esempio nell’accoppiamento, nella saldatura o nell’incollaggio;

  4. nella movimentazione, ad esempio nell’afferraggio con manipolatori [] o su pallet o AGV [], [];

  5. nell’imballaggio o confezionamento, nell’applicazione di segni di riconoscimento (etichette, codici a barre, micropunzonature) [];

  6. nello stoccaggio, ad esempio nello scarico dalla linea, per determinare le posizioni libere in magazzino, per posizionamenti precisi o per minimizzare lo spazio occupato ottimizzando la disposizione degli oggetti;

  7. nei controlli di qualità (QC, Quality Control) [], [], nelle misure, in test di laboratorio;

  8. per la manutenzione.

La visione artificiale ha lo scopo di riprodurre e automatizzare l’analoga funzione nell’uomo e può operare

Con particolare riferimento alla visione, l’automazione può essere adottata nei seguenti casi:

I vantaggi dell’automazione sono:

In quasi tutti i settori sono già presenti applicazioni della visione artificiale, con un’apprezzabile estensione rispetto a [] e si possono ricondurre a due tipologie: controllo del processo e del prodotto. Il controllo del processo può avvenire nei seguenti modi:

  1. attraverso un controllo sull’ambiente, ad esempio, per la sicurezza, verificando la presenza di personale in aree a rischio o seguendo la posizione di un AGV (Automated Guided Vehicle) [], [];

  2. tenendo sotto controllo i macchinari, ad esempio i pallet lungo una linea, il gripper di un robot, l’alimentazione pezzi o il magazzino di una macchina utensile;

  3. tramite un controllo sul prodotto che consente un feedback sul processo.

Se la potenza di calcolo e la complessità dell’algoritmo lo consentono, il sistema può operare in tempo reale (real-time), altrimenti è possibile effettuare dei controlli a campione, ad esempio ogni X pezzi o ogni Y secondi, o ancora, nel caso più sfavorevole, a posteriori.

In relazione all’attività della macchina, il controllo può avvenire in linea di produzione (on-line) o fuori linea (off-line), ad esempio in laboratorio; nel primo caso può avere luogo durante la lavorazione (in process) o a macchina ferma, prima dell’inizio, ad operazione conclusa o in un intervallo tra due operazioni.

I controlli possono essere adottati in produzioni automatiche, semiautomatiche o manuali. I tipi di controlli con un sistema di visione tridimensionale sono:

 

Sono state indicate alcune possibili classificazioni riguardanti l’impiego dei sistemi di visione tridimensionale, in alcuni casi valide per i sistemi di visione anche in campo bidimensionale o per controlli di altro tipo, con sensori diversi o per l’automazione in generale.

È possibile ottenere qualsiasi combinazione, associando un tipo di controllo (ad esempio localizzazione), una tecnologia (saldatura) e una fase produttiva (assemblaggio), e definendo le modalità di applicazione (alimentazione semiautomatica pezzo, in process).

Esaurire tutte le possibilità nel contesto di questo articolo sarebbe impossibile e di scarso interesse. Verranno pertanto indicati di seguito solo alcuni casi salienti a titolo di esempio, con i necessari riferimenti per i dettagli tecnici. Nei capitoli successivi verrà fornita una classificazione delle principali tecniche e degli algoritmi impiegati per la visione tridimensionale.

      1. La visione tridimensionale nel montaggio

Il montaggio automatico è un processo tipicamente tridimensionale in cui in generale un manipolatore (braccio robotizzato) movimenta parti (perno, peg) per accoppiarle con altre (fori, hole) in moto su pallet (problema peg-in-hole). In generale le attrezzature impiegate sono dotate della precisione necessaria per realizzare l’operazione, tuttavia per situazioni critiche (parti costose o delicate) o per fornire maggiore flessibilità al sistema, può avere interesse avere un maggior controllo sul processo. In [] è descritto un sistema, basato su singola telecamera, in grado di rilevare la posizione di un perno rispetto ad un foro, entrambi di caratteristiche geometriche note, al fine di fornire eventuali correzioni o un allarme in caso di anomalie.

In [] è indicato un metodo per aumentare la precisione nella localizzazione di punti in moto lungo traiettorie note che consiste nell’eseguire un’interpolazione con i minimi quadrati per trovare la traiettoria ideale e viene indicato il modo di proiettare poi i punti, precedentemente acquisiti, per ottenerne una migliore stima.

Si può sfruttare un sistema di visione tridimensionale in tutte le fasi di un accoppiamento robotizzato, con i compiti seguenti.

 

º Prima dell’accoppiamento:

  1. scelta del pezzo da afferrare, riconoscimento [], [];

  2. tracking durante lo spostamento del gripper del robot per verifica e eventuale correzione [], [], [].

  3. localizzazione, per impostare lo spostamento del robot come differenza tra la posizione effettiva attuale del gripper e le coordinate del pezzo da afferrare;

  4. verifica che l’afferraggio è avvenuto correttamente;

  5. tracking per verifica e eventuale correzione, durante lo spostamento, del gripper con il pezzo.

¾ Durante l’accoppiamento:

  1. localizzazione del "foro";

  2. localizzazione e eventuale correzione della posizione del "perno" rispetto al "foro" (o viceversa);

  3. controllo della deposizione di materiale come lubrificanti, colla, sigillanti.

 Dopo l’accoppiamento: verifica finale che tutto è avvenuto come previsto.

 

Il robot ARI, di sembianze umane, descritto in [], è in grado di apprendere, osservando attraverso il sistema di visione stereoscopico di cui è dotato, una sequenza di montaggio di semplici parallelepipedi e di correggere eventuali errori di posizione delle due braccia. Il sistema implementa un algoritmo del tipo di quello descritto successivamente, schematizzato in Figura 4, individuando i vertici e i segmenti dei contorni.

In [] è descritta un’applicazione dell’AI per il riconoscimento che richiede la preventiva localizzazione degli oggetti per l’estrazione dei "momenti", cioè dei parametri geometrici necessari.

      1. Le operazioni robotizzate

In tutte le operazioni in cui è presente un braccio robotizzato, come nella saldatura, nella verniciatura o con una testa di taglio, è possibile riprodurre lo schema indicato nel paragrafo precedente introducendo le eventuali semplificazioni.

Le prime applicazioni industriali della visione artificiale per rendere flessibile una linea robotizzata erano limitate al campo bidimensionale, come il sistema modulare descritto in [], in grado sia di localizzare che misurare oggetti su un piano o in [], in cui le feature estratte da immagini binarie ricavate on-line vengono confrontate con quelle ricavate preventivamente, corrispondenti a diverse possibili posizioni e rotazioni dell’oggetto da riconoscere e afferrare su un piano.

A differenza della robotica in cui le principali applicazioni della visione tridimensionale sono nella navigazione, nel riconoscimento e nella coordinazione hand-eye, in campo industriale le stesse informazioni vengono sfruttate prevalentemente per la localizzazione e la misura di oggetti. Tuttavia non mancano eccezioni. Ad esempio, per quanto riguarda il riconoscimento e la navigazione: in [] è descritto un metodo per ridurre le ambiguità nell’identificazione (pattern recognition []), associata alla manipolazione; nel controllo della traiettoria di AGV, è possibile sfruttare il vantaggio di operare modifiche sull’ambiente artificiale di un’industria [].

Il sistema di visione tridimensionale può essere impiegato in concomitanza con un robot, oltre che on-line, come appena indicato, off-line anche nelle seguenti attività:

      1. La visione tridimensionale nel controllo di qualità (QC)

Il QC ha un ruolo fondamentale nella produzione industriale. La visione artificiale si propone come tecnica per il QC e può essere applicata nei casi in cui è richiesto un controllo di tipo visivo incluso tra quelli indicati in precedenza. I controlli sono atti a []:

e possono essere basati su parametri qualitativi o quantitativi. La determinazione dei parametri avviene in una prima fase: l’ispezione.

Il risultato del QC in generale può essere una classificazione, cioè una suddivisione in gruppi omogenei per classi di merito o per livello di difettosità che può comportare o meno lo scarto del pezzo (Figura 1).

 

Figura 1 Il flusso informativo in un processo di controllo di qualità

I parametri che possono essere valutati con sistemi ottici, sono:

  1. parametri geometrici, ad esempio forme e dimensioni con le relative tolleranze;

  2. microgeometrici, ad esempio la finitura superficiale che può anche essere valutata con tecniche di visione ricorrendo a particolari tipi di illuminazione come indicato in [], [];

  3. parametri estetici, come colore, tessiture, e loro distribuzione;

  4. i parametri chimico - fisici possono essere anch’essi valutati tramite visione artificiale, se rilevati con particolari tecniche che forniscono come output delle immagini.

È possibile ottenere immagini relative a fenomeni tridimensionali con tecniche quali:

quindi non necessariamente di tipo ottico, ma che danno come risultato una mappa bidimensionale che può essere trattata con le tecniche di elaborazione delle immagini (image processing), disciplina alla base della visione artificiale, con l’elettronica e l’ottica.

Il processo di controllo con un sistema di visione si articola nelle seguenti fasi:

In fase di creazione del modello (off-line):

  1. esplicitazione dei criteri di valutazione se impliciti;

  2. scelta dei parametri meglio atti ad esprimerli quantitativamente attraverso campioni di riferimento;

  3. quantificazione degli intervalli, determinazione di soglie;

  4. individuazione delle classi, livello di accettazione, ecc.

In fase operativa (on-line)

  1. acquisizione delle immagini ed eventuale pre-processing;

  2. estrazione parametri;

  3. confronto con le soglie

  4. output

Le fasi 1. e 2. si considerano appartenenti al processo di ispezione, le fasi 3. e 4. alla classificazione propriamente detta.

Quando possibile si cerca di ricondurre un problema tridimensionale ad uno bidimensionale, per la semplificazione e conseguentemente per le migliori prestazioni ottenibili a parità di hardware.

In [] un problema tridimensionale come l’individuazione di difetti su una superficie toroidale, viene ridotto ad un problema bidimensionale in quanto, nell’acquisire lo sviluppo della superficie attraverso la rotazione attorno all’asse, le modalità di proiezione avvengono sempre nelle stesse condizioni e quindi è possibile stabilire una corrispondenza diretta tra dimensione del difetto in 3D e area misurata sull’immagine relativa (Figura 2).

 

Figura 2 - Immagine monocromatica di due o-ring (quello sinistro è lacerato) di cui viene eseguito un controllo di qualità tramite un sistema di visione

La maggior parte dei problemi legati al QC presenti in letteratura sono di tipo bidimensionale o ridotti a problemi bidimensionali, che trascendono le finalità di questa trattazione, ad eccezione della valutazione delle tolleranze geometriche, per cui il problema si riconduce al campo della metrologia affrontato nel paragrafo successivo.

In [] vengono controllate le tolleranze geometriche di profili ellittici appartenenti a palette di turbina attraverso la definizione della scelta ottimale dei punti di controllo e di una norma per valutare l’errore. In [] è descritto un sistema per l’ispezione di tubi di grosse dimensioni.

      1. La visione tridimensionale nella metrologia

Il problema principale nei controlli dimensionali è l’esigenza di precisioni elevate che evidenzia le attuali limitazioni dei sensori disponibili sul mercato.

Se si prende a riferimento il contorno di un oggetto, bisogna tenere presente che il gradiente di luminosità interessa più di un pixel del contorno per varie ragioni, tra cui:

  1. messa a fuoco non ottimale;

  2. fenomeni di riflessione della luce sull’oggetto;

  3. interazioni tra gli elementi sensibili del CCD.

Di conseguenza per valutare la precisione di un sistema di visione tridimensionale e di un algoritmo, che può essere espressa in mm3/pixel per tenere conto del volume di lavoro, bisogna tenere conto che, come illustrato precedentemente, lo spessore dei contorni non è unitario, e, supponendo che sia ad esempio di 3 o 4 pixel, si riduce proporzionalmente la risoluzione effettiva. La ricerca del contorno può essere migliorata, in questo caso, con un’operazione di thinning o scegliendo un altro filtro opportuno che tenga conto dell’entità dei gradienti che interessa rilevare [].

Esistono in letteratura molteplici metodi per migliorare la risoluzione spaziale, due dei quali riguardano direttamente il rapporto mm3/pixel e consistono: (1) nell’aumentare il denominatore o (2) nell’agire sul numeratore.

  1. Il metodo più semplice consiste nell’aumentare la risoluzione dei sensori, che comporta costi maggiori e presenta le limitazioni delle attuali tecnologie di produzione del silicio.

  2. È possibile aumentare virtualmente la risoluzione spaziale riducendo l’area inquadrata, ad esempio osservando il campo con più telecamere, oppure aumentando l’ingrandimento in modo che l’oggetto osservato riempia tutta l’immagine.

È possibile inoltre eseguire interpolazioni sui dati disponibili facendo riferimento a primitive geometriche note, quali archi di cerchio, intersezioni tra segmenti, ecc. Se si considera ad esempio un contorno rettilineo è possibile determinarne la posizione in maniera più accurata considerando la retta dei minimi quadrati che interpola i punti del contorno [], []. In tal modo è possibile raggiungere risoluzioni subpixel. Vedere anche [] per una più ampia trattazione.

A titolo di esempio, si riporta un caso semplice: la determinazione dell’ascissa di un contorno verticale, dati N punti di ascissa xi appartenenti al contorno, rilevati con precisione p, ad esempio pari ad 1 pixel (± ½ pixel). L’errore risultante sul valore medio m è pari a dell’errore sul singolo campione p, assumendo, ipotesi generalmente accettabile, una distribuzione normale degli errori.

Un metodo originale che sfrutta questo principio, basato sulla localizzazione di ellissi, è descritto nella parte II [] di questo articolo.

Un altro metodo consiste nel ricorrere ad acquisizioni multiple nei seguenti modi:

Un aspetto interessante delle applicazioni di visione tridimensionale è che sono "scalabili", quindi uno stesso algoritmo applicato con risoluzione dell’ordine del metro [] può essere applicato a risoluzioni dell’ordine del millimetro o del micron (Figura 3) e ciò non vale solo per la metrologia, ma anche per la localizzazione, il tracking, ecc.

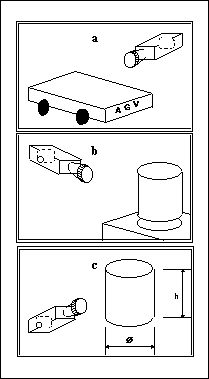
Figura 3 - "Scalabilità" della risoluzione di un algoritmo tridimensionale: (a) tracking di AGV, (b) assemblaggio robotizzato, (c) controllo dimensionale

Sono possibili anche interazioni tra una macchina di misura a coordinate (CMM, Co-ordinates Measuring Machine) e un sistema di visione tridimensionale, ad esempio in [] vengono sfruttate le informazioni sulla posizione dell’oggetto da osservare nel piano di lavoro della macchina per riconfigurare il programma di misura.

Per trattare superfici, anche di forma complessa, si ricorre a particolari tecniche di illuminazione strutturata, trattate nel capitolo 4.

La rilevazione di superfici ha interesse anche nel reverse engineering [].

      1. Visione tridimensionale e CAD

I dati relativi al modello CAD di un oggetto possono viaggiare in due direzioni:

Nei programmi CAD evoluti è possibile descrivere il lay-out di una stazione e simulare il processo per valutare la configurazione ottimale di robot e anche di un eventuale sistema di visione.

      1. La visione tridimensionale nel Tool Condition Monitoring (TCM)

In una rassegna di sensori per il controllo dello stato dell’utensile nelle lavorazioni per asportazione di truciolo del 1983 [], la visione artificiale non è citata. È presente in rassegne successive [] (1988); nella più recente [] è indicato come prospettiva per le lavorazioni automatiche alle macchine utensili, l’impiego dei "sensori intelligenti", cioè in grado di fornire molteplici informazioni e dotati della capacità di apprendere, come nel caso dei sistemi di visione artificiale. In [] è presente un’ampia raccolta di titoli (oltre 500) sul TCM. Attualmente la principale ragione dell’impiego limitato in ambito industriale è legata agli elevati costi e alla complessità rispetto ad altri sistemi, anche indiretti, ugualmente efficaci. E’ inoltre da tenere presente, specialmente in questo campo di applicazioni, l’aggressività dell’ambiente industriale nei confronti delle lenti e dei circuiti elettronici (polvere, umidità, vapori, vibrazioni, rumore elettrico, ecc.). Un nuovo impulso al settore è legato all’introduzione delle macchine di registrazione (pre-setting) di ultima generazione, basate sull’uso di tecniche di visione bidimensionale [].

Il problema del TCM con i sistemi di visione è stato ampiamente trattato in letteratura e i metodi impiegati possono essere ricondotti ai seguenti approcci:

In [] viene indicato un metodo originale che permette di estrapolare le caratteristiche tridimensionali dell’utensile o della placchetta a partire da una sola vista sfruttando le informazioni geometriche note (angoli caratteristici).

In [] viene descritto un metodo per il TCM on-line su frese periferiche attraverso l’impiego di un sensore lineare che consente di acquisire le immagini del fianco dei denti anche ad alta velocità di rotazione.

    1. Caratteristiche dei sistemi di visione tridimensionale

      1. Il colore nella visione tridimensionale

L’impiego di immagini a colori è relativamente recente per la disponibilità e i costi delle telecamere e soprattutto per l’esigenza di maggiore potenza di calcolo dovuta all’elaborazione di tre immagini in luogo di una, in quanto, come è noto, per la legge della composizione dei colori sono necessarie e sufficienti tre bande (colori fondamentali o codifiche HSV [], []). Le immagini digitali a colori possono essere ottenute con telecamere basate sulle seguenti tecnologie:

In alternativa ad una telecamera a colori può essere sufficiente un filtro ottico per evidenziare o eliminare la componente che interessa.

Il colore non ha dirette implicazioni per la ricostruzione tridimensionale, ma può portare vantaggi per la segmentazione [] e il riconoscimento [].

      1. Possibili configurazioni di un sistema di visione tridimensionale

 

Gli elementi costitutivi di un sistema di visione

Dipendono dal tipo di impiego e in generale sono:

 

La configurazione di un sistema di visione tridimensionale può essere ad una, a due o più telecamere. Se la scena da osservare non è nota, cioè non è possibile contare su informazioni pregresse, come spesso accade in ambienti strutturati come quello industriale, sono necessarie almeno due telecamere, in quanto due proiezioni di un punto permettono di conoscerne la posizione nello spazio. Esistono anche configurazioni artificiose con l’impiego di specchi, come in [] in cui è possibile la localizzazione con una sola vista che include l’oggetto e la sua immagine riflessa.

        1. Sistemi di visione stereoscopici

          2. I due piani immagine possono essere disposti in qualsiasi modo ad osservare la scena. Naturalmente è conveniente massimizzare il numero di punti di interesse osservati da entrambe, ma questo può essere perseguito sia con gli assi ottici paralleli che incidenti.

          Due telecamere con gli assi tra loro ortogonali e coincidenti con quelli del sistema di riferimento forniscono la massima precisione lungo detti assi.

          Inversamente due telecamere ad assi paralleli (come nell’uomo) consentono una minore risoluzione, e quindi precisione, nel rilevare la profondità, ma presentano alcune peculiarità di tipo geometrico e rappresentano la soluzione migliore se non è nota a priori la posizione degli oggetti da osservare.

           

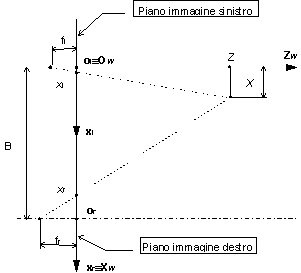
          Figura 4 - Visione stereoscopica con telecamere ad assi paralleli

          Come si può osservare dall’esempio in Figura 4, in cui senza perdere di generalità il sistema di riferimento principale (Ow, Xw, Yw, Zw) (solidale al mondo, world) coincide con il sistema di riferimento solidale alla telecamera sinistra (ol, xl, yl), note le distanze focali fl e fr delle due telecamere, è sufficiente conoscere la distanza B (Baseline) tra gli assi ottici, per determinare completamente il sistema, cioè la posizione nello spazio del punto (X, Y, Z), note le proiezioni (xl, yl) e (xr, yr); le relazioni geometriche con yl e yr sono analoghe ruotando gli indici e con le dovute accortezze sui segni delle terne di riferimento.

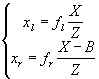
          nel caso in cui le telecamere sono uguali o con singola telecamera in moto,

          fl = fr = f

          da cui

          dove

          d = xr - xl

          è definita disparità.

        2. Sistemi di visione a più telecamere

L’aggiunta di più viste consente diverse possibilità: incrementare la precisione del sistema inserendo nel modello tutte le viste [], [] oppure operare con le telecamere a due a due secondo le seguenti opzioni:

  1. vengono impiegate numerose telecamere per coprire un vasto volume di osservazione in modo da avere, per ciascuna coppia, una risoluzione sufficiente;

  2. può essere necessario ovviare ad eventuali "occlusioni", ad esempio quando nella scena vi sono parti in movimento. L’aggiunta di una telecamera rappresenta un aumento del costo e della complessità, quindi a questa soluzione si ricorre quando non è possibile posizionare due sole telecamere in modo da avere, in tutte le condizioni, il campo sgombero da ostacoli. In [] la terza vista consente di superare il problema della riflessione luminosa che crea un errore nella localizzazione di oggetti con superficie metallica;

  3. possono essere sfruttate viste più favorevoli per migliorare la precisione, facendo in modo che il piano immagine e quello osservato risultino all’incirca paralleli. Ad esempio, osservando uno spostamento è bene che avvenga perpendicolarmente all’asse ottico, analogamente per il piano che contiene superfici da misurare o rilevare;

  4. per valutare l’errore commesso per confronto tra i dati ottenuti con le diverse coppie di telecamere o per ridondanza, per ovviare a guasti o ad altri eventi non prevedibili, in situazioni critiche (ambienti ostili, non accessibili).

In [] viene indicato un algoritmo lineare in cui la proiezione ortogonale su tre viste si dimostra condizione necessaria e sufficiente per trovare un’unica soluzione al problema della ricostruzione del moto. In [] è stato mostrato che, con un algoritmo non - lineare, sono necessarie le corrispondenze di 4 punti, appartenenti ad un corpo rigido, su tre proiezioni ortogonali.

        1. Sistemi di visione tridimensionale a singola telecamera

Nel caso particolare, comunque molto diffuso in ambito industriale, in cui sono note le caratteristiche geometriche di un oggetto osservato, è possibile conoscerne la posizione attraverso una sola vista [], (in [] con rete neurale) e viceversa, data la posizione, è possibile eseguire delle misure [].

È interessante notare che più viste possono essere ottenute anche con una singola telecamera nei seguenti casi:

in entrambi i casi, la scena deve rimanere invariata tra i due istanti in cui avviene l’acquisizione dell’immagine. Se le caratteristiche ottiche della telecamera non mutano (ad esempio fl = fr, in Figura 4), la calibrazione riguarda una sola telecamera. In questo modo si può ottenere un sistema stereoscopico con lo spostamento di una singola telecamera, associando coppie di viste consecutive, come in [].

Nel caso in cui la scena osservata vari, il problema diventa l'analisi del movimento, che può essere trattato sia per il caso stereo, sia nel caso di singola telecamera.

Per il principio della relatività galileiana le leggi di proiezione tridimensionale valgono sia nel caso di telecamera in moto che di oggetto in moto rispetto ad essa, da cui si ottengono rispettivamente le tipiche configurazioni: ego-docking e echo-docking nei casi in cui un robot sfrutta le informazioni di una telecamera a lui solidale o che l’osserva dall’esterno [], []. Il primo caso è più frequente nella robotica e comprende la configurazione hand-eye, il secondo in ambiente industriale.

In tutti i casi trattati anche nei paragrafi precedenti, ma, in particolare con singola telecamera, [], [], [], è possibile ricorrere ad illuminazione strutturata (capitolo 4).

      1. Calibrazione di un sistema di visione tridimensionale

Il problema della visione tridimensionale consiste nell’associare ai pixel della o delle immagini le corrispondenti coordinate spaziali. L’intero processo deve essere preceduto dalla "calibrazione" (calibration) del sistema. Il problema presenta un approccio deterministico non - lineare che si basa sui principi dell’ottica [] e della geometria dello spazio e sulla conoscenza dei modelli dei sistemi di ripresa. Esiste un’ampia bibliografia sull’argomento [], [], [], [], [], [], [], [] e l’analisi di questi aspetti si presenta delicata in quanto condiziona la precisione e al limite il successo di un algoritmo di visione. È possibile calibrare un sistema (uncalibrated) contemporaneamente al suo impiego on-line, sia nel caso di sistemi stereo che a singola telecamera []. Ciò ha prevalentemente interesse nella robotica in cui la configurazione può mutare nel tempo.

 

Figura 5 - Fasi di calibrazione off-line e di esecuzione on-line di una generica applicazione di visione tridimensionale

In Figura 5 è indicato lo schema relativo al funzionamento di un sistema di visione e sono evidenziate la fasi di "addestramento" e l’esecuzione. I parametri del modello che descrive il comportamento del sistema di visione si distinguono in interni (o intrinseci) ed esterni (o estrinseci).

Vengono ora elencati i principali parametri interni nell’ordine in cui devono essere determinati, dal momento che i primi che vengono calcolati sono necessari ai successivi. In alcuni casi, per raggiungere precisioni particolarmente spinte, può essere opportuno rieseguire la determinazione utilizzando i valori ricavati nell’iterazione precedente.

  1. Rapporto tra i lati dell’immagine o rapporto d’aspetto (aspect ratio). Quando questo parametro non è unitario, un cerchio appare come un’ellisse e un quadrato appare come un rettangolo. Può subire alterazioni in funzione dello standard di trasmissione del segnale video, in particolare della frequenza di scansione dell’immagine, per cui il numero di colonne e di righe non mantiene una proporzione esatta. Nel caso del sistema televisivo NTSC (americano) la sproporzione è presente esplicitamente nella definizione dello standard che prevede pixel rettangolari.

  2. Posizione dell’asse ottico. In prima approssimazione coincide con il centro dell’immagine e dipende dal non corretto allineamento tra asse della telecamera e dell’obiettivo.

  3. Distorsione ottica delle lenti. Questo fenomeno, a seconda se di segno positivo o negativo, si traduce nell’effetto cuscino o barile. La distorsione radiale è quella prevalente tra le distorsioni presenti nei sistemi ottici, i cui altri effetti vengono generalmente resi di ordine di grandezza inferiore a questo attraverso un opportuno studio del treno di lenti.

  4. Distanza focale. È definita come la distanza tra il centro del sistema ottico e il piano di proiezione dell’immagine. Nella realtà varia in funzione della posizione relativa oggetto osservato - lente, ma nelle applicazioni pratiche può essere considerata costante come nel modello di telecamera pinhole schematizzato in Figura 4.

  5. Fattore di ingrandimento o scala. Dipende dal tipo di lenti usate, può essere maggiore o minore dell’unità. In questo fattore è possibile anche inglobare le dimensioni del pixel espresse nelle unità di misura del sistema di riferimento principale (generalmente mm) in modo da operare in un sistema coerente.

I principali parametri esterni sono quelli che definiscono la configurazione geometrica, cioè la posizione e l’orientamento dei piani di proiezione dell’immagine rispetto al sistema di riferimento principale, solidale alla scena osservata.

I parametri indicati sono tutti necessari sia per applicazioni bidimensionali sia tridimensionali. Per le prime può risultare più semplice la determinazione di alcuni parametri del modello come mostrato nel seguito.

I metodi per l’acquisizione dei parametri possono essere di due tipi: diretti e indiretti (Figura 5). Nelle applicazioni pratiche di visione si ricorre generalmente a questi ultimi, essendo i primi di interesse nel campo dell’ottica o di studi specialistici sui dispositivi impiegati (sensori, telecamere, ecc.). Generalmente è necessario acquisire dei punti di controllo distribuiti nello spazio, poiché se appartenenti ad uno stesso piano il sistema di equazioni risulta indeterminato.

I metodi numerici [] consistono nel definire una trasformazione, invertibile, da punti nello spazio a punti proiezione nei piani immagine, espressa genericamente dalla relazione

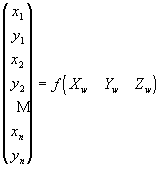
In [] e [] è stato proposto un particolare tipo di metodo numerico, evidenziato nello schema di Figura 5, basato sull’utilizzo di una rete neurale. Nella fase di apprendimento vengono forniti contemporaneamente al sistema sia i parametri interni, sia i parametri esterni.

    1. Algoritmi di visione tridimensionale

Fissati i sistemi di riferimento solidali ai piani di proiezione e al volume in esame, le corrispondenze possono essere descritte attraverso modelli, di diversa complessità, che tengono conto dei dispositivi usati per l'acquisizione delle immagini. Tale trasformazione è biunivoca, come indicato in Figura 5, ma nel campo della visione artificiale, generalmente ha interesse il solo problema di ricostruzione tridimensionale, cioè in un solo senso. Il problema della visione tridimensionale può essere risolto in vari modi basati sulla triangolazione, tra cui quelli descritti in [], [], [] che propongono algoritmi diversi o che introducono nel modello ipotesi diverse. Alla fase di ricostruzione 3D, indicata in Figura 5, seguono le eventuali fasi di localizzazione, riconoscimento, misura, ecc. Nello stesso schema sono rappresentate le alternative tra sistemi stereo e basati su singola vista e il caso delle acquisizioni multiple precedentemente trattato.

Il modello di telecamera pinhole (Figura 4) è generalmente accettato. Un’ipotesi che può essere introdotta nel modello di visione tridimensionale riguarda la "prospettiva debole" [] che consiste nell’assumere costante la distanza degli oggetti dalla telecamera, ad esempio la coordinata Z di Figura 4, al fine di rendere il problema lineare. In [] vengono illustrate le condizioni in cui questa ipotesi risulta accettabile e applicate al caso di tre telecamere in []. In alternativa alla proiezione prospettica [], viene proposto il metodo delle proiezioni ortogonali con relativa trattazione analitica [], [].

L’illuminazione strutturata [], [], cioè la proiezione di profili o motivi (pattern) luminosi noti e periodici, ad esempio griglie o lame di luce in movimento, ha un ruolo fondamentale nella visione 3D, in quanto consente di ricostruire anche superfici irregolari, fatta eccezione naturalmente, per le parti in sottosquadro, non illuminate o comunque non visibili.

Le tecniche di elaborazione del pattern sono di vario tipo:

 

Nella parte II [] di questo articolo verranno descritti, anche a titolo di esempio, due algoritmi tridimensionali originali. Il primo è basato su singola telecamera con tecnologia neurale, utilizza le primitive geometriche presenti nell’immagine e può essere impiegato per la localizzazione. Il secondo riguarda un approccio innovativo al problema del match e consente la ricostruzione di una scena a partire da una coppia di immagini stereo.

    1. Conclusioni

È stata presentata una possibile classificazione delle applicazioni dei sistemi di visione tridimensionale ai processi produttivi con riferimenti a casi salienti.

La tecnologia in esame presenta potenzialità che la rendono pervasiva e consente elevata flessibilità dai punti di vista seguenti:

La penetrazione è favorita nei settori a più alta tecnologia e dipende non solo dalla economicità, ma, soprattutto, dall’affidabilità. La disponibilità di sistemi dotati di tali caratteristiche per impieghi in campo industriale è legata allo sviluppo della ricerca sulla visione 3-D, che è, per molti aspetti, ancora un problema aperto.

    1. Bibliografia