- Sistemi di visione:
Visione Tridimensionale nei Processi di Produzione - Applicazioni
Michele Lanzetta
Dott. Ing. Michele Lanzetta - Dottore di Ricerca in Automazione e Robotica Industriale - DIP - Dipartimento di Ingegneria della Produzione - Università degli Studi di Pisa - E-mail: m.lanzetta@ing.unipi.it
Vengono proposti due algoritmi. Il primo, basato su primitive geometriche, per determinare la posizione 3-D di oggetti osservati con un sistema di visione di tipo neurale a singola telecamera attraverso l’estrazione di archi ellittici dai contorni. Il secondo rappresenta un approccio innovativo al problema del match e consente di ricostruire qualsiasi scena osservata da un sistema stereoscopico di cui è stata eseguita la calibrazione.

- Introduzione
Nella parte I [] di questo articolo è stata fornita un’ampia rassegna di applicazioni della visione 3-D in campo industriale ed una schematizzazione in funzione del tipo di impiego e della configurazione adottata. Sono stati descritti metodi di calibrazione e algoritmi implementati con la classificazione dei principali approcci presenti nella letteratura recente.
In questa parte II vengono proposti due algoritmi di impostazione diversa tra loro che presentano potenzialità interessanti per applicazioni in campo industriale.
Il primo può essere impiegato per rilevare la posizione di oggetti nello spazio, è caratterizzato dall’impiego di un metodo neurale e utilizza una sola telecamera, aspetti che conferiscono semplicità d’uso e riduzione della complessità del sistema. Per l’"addestramento" è sufficiente una serie di esempi ed è possibile la validazione delle prestazioni ottenibili (capitolo 2).
Il secondo algoritmo è nato [] ed è stato sviluppato presso l’Università di Stanford e rappresenta un’interessante soluzione per un problema ancora aperto: la stereopsi (capitolo 3).
- Un algoritmo neurale per la localizzazione tridimensionale con singola telecamera, basato su primitive geometriche
Possibili applicazioni
Questo primo algoritmo si basa sull'utilizzo di reti neurali artificiali (ANN, Artificial Neural Networks) [] per la localizzazione di oggetti tramite un sistema di visione monoscopico (¹
stereoscopico) [].
Come illustrato nella parte I [], è sufficiente un solo dispositivo di ripresa, anche nel caso di visione tridimensionale, a condizione che siano note, oltre ai dati di calibrazione, le caratteristiche geometriche degli oggetti osservati.
Il metodo descritto può essere esteso a corpi di forma qualunque, ed è stato testato in un caso pratico relativo a corpi cilindrici, osservati genericamente come ellissi da parte di una telecamera.
L'interesse di questo algoritmo nel campo della produzione deriva dal fatto che la presenza di oggetti cilindrici o di parti cilindriche, come fori e smussi, è molto comune in campo industriale []. Le applicazioni tipiche riguardano le operazioni robotizzate e in particolare la localizzazione. Il sistema descritto è in grado di rilevare la posizione di un corpo nello spazio e l’eventuale errore per fornire la correzione necessaria.
Il principale vantaggio dell’approccio neurale è che tramite l'addestramento è possibile fornire al sistema sia le informazioni necessarie alla calibrazione, sia le informazioni geometriche, inoltre il sistema può essere programmato facilmente anche da personale non specializzato [], [].
- L’algoritmo

Figura 2 Estrazione di caratteristiche geometriche (feature) dall'immagine
L’algoritmo si articola schematicamente nelle seguenti fasi (Figura 2):
- Acquisizione di n immagini con posizione e orientamento dell'oggetto noti.
- Estrazione delle feature.
- Addestramento delle reti neurali.
Tenendo conto delle considerazioni relative alle forme più comuni presenti in campo industriale e nel caso esaminato il flusso logico può essere così dettagliato.
- Acquisizione.
- Estrazione dei contorni.
- Determinazione delle ellissi dei minimi quadrati.
- Interpolazione dei dati ricavati dalle n immagini.
- Addestramento.
In fase on-line, il sistema fornisce in uscita la posizione 3D degli oggetti osservati che può essere confrontata con quella misurata con l’attrezzatura sperimentale per determinare la precisione del sistema. Lo schema riassuntivo di Figura 3 può essere esteso al caso generale di localizzazione con un sistema di visione artificiale di tipo neurale.
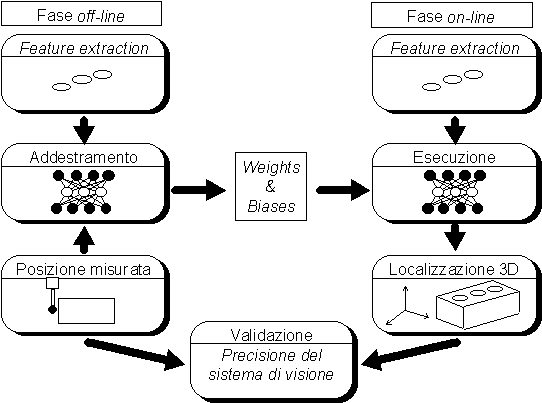
Figura 3 Fasi off-line e on-line di un algoritmo neurale di localizzazione
- Pre-processing
Nelle prove effettuate su pezzi cilindrici anche sporchi di olio e parzialmente ossidati (Figura 1), una illuminazione concentrata della base, piana e metallica, consente di ottenere immagini ad alto contrasto.
Al fine di ridurre il rumore, se presente, viene eseguito in sequenza uno smoothing e uno sharpening il cui risultato è quello di esaltare i contorni []. I filtraggi con un kernel 3´
3, utilizzati per ottenere gli effetti descritti in questo paragrafo, sono indicati in Tabella 1.
Tabella 1 - Maschere di convoluzione
|
smoothing
|
sharpening
|
laplacian
edge-detection |
|
1 |
2 |
1 |
|
-1 |
-1 |
-1 |
|
-1 |
-1 |
-1 |
|
2 |
4 |
2 |
|
-1 |
-9 |
-1 |
|
-1 |
-8 |
-1 |
|
1 |
2 |
1 |
|
-1 |
-1 |
-1 |
|
-1 |
-1 |
-1 |
Dato l'elevato contrasto delle immagini, si procede poi ad una binarizzazione in cui l'eventuale presenza di parti scure all'interno della faccia del cilindro può essere all'occorrenza eliminata tramite un’operazione di opening.
Per l'estrazione dei contorni (edge-detection), viene utilizzato un filtro laplaciano ottenendo il risultato illustrato in Figura 1.
Per ridurre la dimensione delle immagini trattate, e quindi lo spazio di memoria necessario, queste vengono convertite in bitmap binarie (0, 1). In questo caso i pixel bianchi, a livello 1, vengono estratti dall'immagine e memorizzati in una matrice di coordinate.
- Estrazione delle feature
L'algoritmo trattato si basa sull'estrazione di caratteristiche (feature) dall'immagine che descrivono l’oggetto, che consentono di determinarne la posizione e l'orientamento relativo.
Il vantaggio di utilizzare archi di ellissi o ellissi complete rispetto ad operare su primitive più semplici come segmenti, anch’essi molto diffusi nelle applicazioni industriali, è che le prime sono in grado di fornire anche informazioni sul fattore di scala, quindi sulla distanza (posizione) degli oggetti, mentre la determinazione degli estremi di segmenti è affetta da maggiore incertezza.
Per l'addestramento delle reti neurali vengono utilizzati i parametri dell'equazione implicita

dove h, k sono le coordinate del centro, a, b le dimensioni degli assi e Q
l’angolo, misurato in senso antiorario, formato dall’asse maggiore. In forma sintetica
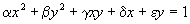
e i parametri a, b, g, d e e esprimono le principali caratteristiche di interesse quali:
- posizione del centro;
- dimensioni degli assi principali;
- orientamento degli assi principali;
- eccentricità;
che hanno un legame diretto con la posizione e l’orientamento dell’oggetto a cui appartiene l'ellisse.
Per calcolare tali parametri viene applicato il metodo dei minimi quadrati alle coordinate dei punti del contorno estratto dal pezzo.
- Architettura della rete neurale
Per ridurre la complessità della rete è necessario separare le informazioni relative alla posizione e all'orientamento del pezzo. Tale operazione è possibile dato che ad un'inclinazione dell'oggetto corrisponde una variazione dell'eccentricità, quindi un effetto geometrico ben definito e rilevabile.
Le reti utilizzate nelle prove sono indicate in Tabella 2.
Tabella 2 - Reti neurali impiegate
|
Tipo di rete |
feed-forward |
|
Algoritmo di
addestramento: |
back-propagation
(Levenberg-Marquardt) |
|
Numero ingressi: |
5 |
|
Funzioni di trasferimento
verso lo strato nascosto: |
lineare pura |
|
Nodi nello strato nascosto: |
5 - 8 |
|
Funzioni di trasferimento
verso l’uscita: |
tangenziale sigmoide |
In ingresso vengono forniti i parametri che definiscono l’equazione implicita dell’ellisse ricavati nel paragrafo precedente, mentre, nel caso esaminato, in uscita si hanno le due coordinate dello spostamento per una rete e la rotazione per l'altra (Figura 4).
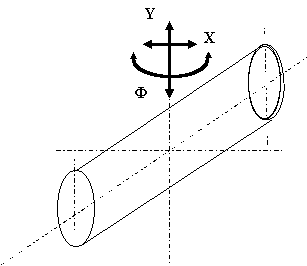
- Prove sperimentali
Alcune prove sperimentali preliminari sono state eseguite per mettere a punto e testare l'algoritmo utilizzando un cilindro Æ
40 mm movimentato tramite il banco di una fresatrice universale in grado di fornire spostamenti e rotazioni con la precisione di 1/100 mm.
Nelle immagini trattate i pixel appartenenti al contorno dell'ellisse sono circa 2.000. Gli stessi risultati, in termini di errore, sono stati ottenuti attraverso diverse scelte arbitrarie di sequenze di punti estraendone 700, mostrando in tal modo che eventuali situazioni di "occlusioni", praticamente riscontrabili nella pratica, non costituiscono una limitazione per l’applicazione dell’algoritmo.
Uno dei vantaggi di questo approccio è che è sufficiente un numero ridotto di acquisizioni di punti noti per addestrare la rete, nel caso particolare 6 posizioni (Tabella 3) e 18 rotazioni (Tabella 4).
Tabella 3
|
Posizioni acquisite (X, Y) [mm] |
|
(0,0) |
(1,2) |
(0,2) |
|
(2,2) |
(2,1) |
(2,0) |
Tabella 4
|
Rotazioni acquisite F
nelle posizioni suindicate |
|
+1.5° |
0° |
-1.5° |
Per l’addestramento della rete è necessario un numero elevato di campioni che sono stati ottenuti interpolando linearmente fino a 100 posizioni intermedie tra due posizioni misurate. Con le (sei) posizioni rilevate suindicate e venti interpolazioni si ottengono 100 ellissi che si sono dimostrate sufficienti per addestrare una rete relativamente alla sola posizione del cilindro.
Per quanto riguarda le variazioni dell'angolo F
, anch’esse vengono interpolate a intervalli di 1/100, per un totale di 600 campioni. La rete addestrata è in grado di generalizzare con errore sull'angolo minore di 0.2° all'interno di un settore di circa 30° contenente le ellissi interpolate.
È stato inoltre mostrato che il problema può essere scomposto e trattato da reti neurali diverse, in parallelo:
- considerando la posizione di più oggetti nella scena separatamente, ad esempio nel caso di accoppiamento di due parti;
- separando le informazioni relative alla posizione e all'orientamento.
In tal modo la complessità della rete neurale necessaria si riduce e conseguentemente nelle applicazioni è sufficiente impiegare hardware di minore potenza.
Il metodo si è dimostrato semplice ed affidabile conseguendo precisioni elevate, nonostante questo sia un limite tipicamente derivante dall'applicazione di reti neurali. Attraverso interpolazioni numeriche ottenute elaborando un numero limitato di acquisizioni è infatti possibile addestrare sufficientemente una rete.
La validazione del metodo risulta affidabile in quanto è possibile testare la rete su una griglia, fitta a piacere, di valori ed evidenziare l’andamento dell'errore. Per la validazione del metodo i campioni (sperimentali e interpolati) sono stati suddivisi in due insiemi, uno impiegato per l’addestramento della rete, l’altro per il test. L’addestramento è stato arrestato in modo da evitare problemi di overfitting [].
- Il problema delle corrispondenze (match) in immagini stereo
- Definizione del problema e possibili approcci
Nel caso dei sistemi stereoscopici, cioè con due o più telecamere, per ricostruire la posizione di un oggetto, prima di eseguire la triangolazione, è necessario compiere le seguenti operazioni, che sono commutative:
- segmentazione, individuazione all’interno di ciascuna immagine di aree o contorni degli oggetti di interesse, ad esempio con i metodi [], [], [], [], []. Le aree individuate possono essere classificate attraverso un’operazione di etichettatura (labelling);
- match, individuazione delle corrispondenze tra punti di immagini associate. Le corrispondenze possono essere espresse sotto forma di disparità associate ad una delle due immagini, cioè valori interi con segno che esprimono la differenza tra le coordinate dei pixel corrispondenti.
In formula
fi(x, y) = d(h, v) : h £
width; v £
height
con
i = l, r
a seconda che ci si riferisca all’immagine di sinistra o di destra (left e right) rispettivamente; width, height rappresentano la larghezza e l’altezza delle immagini; h, v rappresentano il valore delle disparità (horizontal e vertical) e dipendono dalla posizione relativa tra le telecamere e dalla scena osservata. Una schematizzazione del problema è stata riportata anche nella parte I [].
Tale funzione differisce tra le due immagini esclusivamente per il segno, che è a priori noto se è noto quale sia l'immagine di sinistra e di destra. In particolare per le disparità dell'immagine di sinistra fl(x, y) e fr(x, y) dell'immagine di destra sarà
fl ³
0 "
x, y
fr £
0 "
x, y
assumendo la convenzione seguente: con l’origine nel vertice in alto a sinistra dell’immagine.
Nel caso di telecamere parallele ed affiancate
v = 0 "
x, y
e il match può essere compiuto prendendo in esame una riga (scanline) per volta. Nella determinazione delle corrispondenze si possono presentare i seguenti problemi:
- "ambiguità", più punti di un’immagine possono essere abbinati al medesimo punto dell’altra poiché presentano le stesse caratteristiche. Il problema si verifica tipicamente nel caso di tessiture o motivi periodici e per essere risolto richiede l’introduzione di informazioni aggiuntive dall’esterno;
- "occlusioni", riguardano i punti che non hanno corrispondenze nella vista associata poiché risultano ostruiti. Questo tema è ampiamente trattato in bibliografia ma appare tuttora un problema aperto. Per tali punti non è possibile ricostruire la posizione nello spazio in quanto non si dispone di almeno una coppia di coordinate. Nell’algoritmo descritto nel capitolo 3, nel caso di "occlusioni", cioè di punti visibili da una sola telecamera, fi(x, y) assume un valore arbitrario.
Nel caso di incertezza o nell'impiego di più algoritmi in cascata, alla funzione fi(x, y) possono essere associati diversi valori, tra i quali viene poi operata una riduzione o una scelta [].
Per il problema del match tra i punti di due immagini stereo esistono numerosi metodi, ma nessuno appare, al momento, il migliore. È possibile considerare contorni, spigoli (per cui è necessario fare precedere la segmentazione al match) o la sola variazione di luminosità. In quest’ultimo caso esistono due tendenze:
- una codifica sofisticata (come nel caso trattato nel capitolo successivo che adotta il metodo delle "curve intrinseche") a cui segue un match rapido;
- una codifica semplice (ad esempio a partire direttamente dai pixel sull’immagine) su cui viene applicato qualche algoritmo di match.
Un metodo classico per determinare le corrispondenze è dato da []. Questo algoritmo calcola la dissimilarità tra due finestrelle in due immagini, e determina una disparità con risoluzione subpixel che minimizza la dissimilarità.
Il match di tutti i punti appartenenti ad un oggetto, pur risultando un’operazione onerosa in ambiente strutturato, presenta il vantaggio di accrescere notevolmente la precisione e l’affidabilità nel ricostruire la scena.
All'aumentare della complessità, l’ambiguità si riduce. In [] viene descritta una tecnica per ricostruire i contorni in immagini stereo tramite descrittori di Fourier. In [] viene proposta una codifica delle forme contenute in un'immagine attraverso tratti del contorno. La stessa tecnica viene usata anche per la compressione di immagini, pertanto, usando tali elementi, il match può essere compiuto anche su immagini compresse.
I sistemi stereoscopici presentano una proprietà particolare che semplifica notevolmente il problema del match: la definizione [] e uso delle "linee epipolari" [], [], []. In alternativa, esistono altri vincoli, come la somiglianza di contrasto o di orientazione.
Esistono anche metodi basati sull’AI [], che consentono di interpolare tra dati mancanti (in [] con rete di Kohonen); ad esempio in [] viene risolto il problema della corrispondenza tra punti di immagini stereo ricorrendo ad una rete neurale artificiale di Hopfield precedentemente addestrata con altre immagini. Il confronto viene eseguito su singola scanline e il risultato sono le disparità, eventualmente multiple, che poi vengono opportunamente ridotte ad un solo valore.

Figura 5 Coppia di immagini stereo, risoluzione 576´
384´
8 bit, con la scanline "84" evidenziata
- Il metodo delle "curve intrinseche" per il problema del match
Il metodo [] consente di trovare il match tra immagini stereo operando su scanline corrispondenti. Il fatto di operare riga per riga non costituisce una limitazione al metodo in quanto, nota la posizione relativa tra le due telecamere del sistema di visione, o le due posizioni assunte, nel caso di singola telecamera in moto traslatorio, è sempre possibile identificare due linee corrispondenti, a condizione di prenderle lungo direzioni in generale inclinate rispetto agli assi principali dell’immagine, cioè non coincidenti con le righe o le colonne.
Le prove vengono eseguite su singola scanline per mostrare la fattibilità del metodo e le principali caratteristiche.
È possibile calcolare le derivate e gli integrali di ogni ordine per ciascuna scanline (Figura 6). Nel caso discreto, con una sequenza di pixel, ciò vuol dire calcolare i rapporti incrementali o delle sommatorie. Se rappresentiamo in un nuovo dominio due scanline corrispondenti, fissando sulle ascisse i valori dei pixel e sulle ordinate la derivata prima del segnale rispetto ad x, per effetto delle transizioni del segnale su una immagine, chiaro - scuro e scuro - chiaro, l’andamento delle curve nel nuovo dominio, definito "piano delle fasi", è rappresentato da cicli (loop) attorno all’origine (Figura 7) che vengono definite "curve intrinseche".

In generale le differenze tra due scanline sono dovute a variazioni della luminosità B (brightness, del segnale) e del contrasto A (contrast, la sua derivata), alla presenza di rumore di espressione generica n(x) (noise) e distorsioni geometriche a, oltre naturalmente alle disparità d, per cui la luminosità lungo la coordinata x della scanline destra può essere espressa in funzione di quella sinistra con la generica relazione
r(x) = A l(a x + d) + B + n(x)
Nei casi pratici si osserva che, mantenendo il rumore n(x) e le distorsioni geometriche a a livelli ragionevoli, il fenomeno è dominato dalla variazione del contrasto A e della luminosità B tra le due immagini, quindi ciò si traduce nel "piano delle fasi" in una dilatazione (compressione) isotropica con centro nell’origine e una traslazione. Per ridurre l’errore causato dall’offset della luminosità (termine B) è sufficiente un filtraggio a media nulla. Per quanto riguarda invece le variazioni di contrasto tra le due immagini, questo ha un’importante conseguenza nell’applicazione del metodo descritto []: le corrispondenze (match) tra punti si trovano lungo raggi passanti per l’origine degli assi e, analogamente, esprimendo la posizione dei punti nel "piano delle fasi" in coordinate polari, i punti corrispondenti hanno la stessa fase.
La diretta conseguenza del principio affermato è che per determinare il match tra punti appartenenti a due scanline corrispondenti è sufficiente
- rappresentarli nel "piano delle fasi";
- ordinarli in funzione della fase.
Purtroppo l’evidenza sperimentale mostra che l’applicazione di questo semplice e rivoluzionario principio si scontra con un problema pratico che ne complica notevolmente l’implementazione: l’"ambiguità" dei punti che si trovano alla stessa fase ma su loop diversi.
La distanza di detti punti dall’origine non permette di eliminare l’"ambiguità" in quanto spesso punti appartenenti a loop diversi si sovrappongono. In Figura 7 sono rappresentati solo 100 dei 576 punti appartenenti alle scanline "84" delle immagini sinistra e destra di Figura 5. È facile notare come gli andamenti siano "simili" ma è altrettanto evidente la complessità del problema delle corrispondenze in zone, come ad esempio l’intervallo [10-20, 0], in cui si sovrappongono numerosi loop.
Tali loop hanno una particolarità: non contengono l’origine degli assi e vengono definiti "asole".
Un altro importante aspetto riguarda il comportamento dell’algoritmo riguardo le "occlusioni": nel metodo qui descritto comportano la sparizione di tratti di loop o addirittura di loop completi in una delle due "curve intrinseche" e nel caso attuale rimangono irrisolte.

- Evoluzione del metodo
Nel piano delle fasi sono possibili diversi metodi per determinare le corrispondenze. In [] viene valutata la spline che interpola i punti delle curve intrinseche, tuttavia l’interpolazione oltre a costituire un aumento della complessità dell’algoritmo, non ha il vantaggio di aggiungere nuove informazioni utili per il match. In alternativa, viene proposto un metodo che opera su dati discreti, considerando esclusivamente i valori ottenuti dalle immagini originali.
Un ulteriore elemento, che è stato inserito nell’algoritmo per aumentarne l’efficienza, consiste nello sfruttare l’informazione che i punti di una scanline appartengono ad una determinata sequenza che deve essere rispettata nel determinare le corrispondenze.
L’ultima rilevante innovazione riguarda la scomposizione della scanline in tratti più brevi con conseguente riduzione del numero di possibili match da valutare.
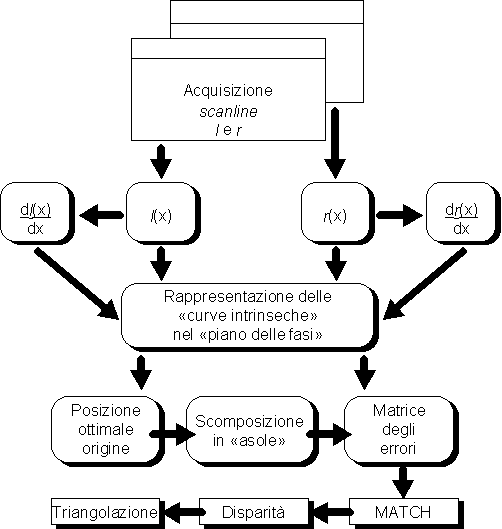
Figura 8 Schema dell'algoritmo proposto per il match: dall'acquisizione della coppia di immagini stereo alla ricostruzione della posizione 3D
L’algoritmo si basa sui seguenti passi (Figura 8):
- scomposizione della scanline in tratti di curva compresi tra due "asole" con il metodo descritto nel paragrafo successivo;
- individuazione delle corrispondenze (punti con uguale fase sulle curve sinistra e destra) eseguita loop a loop;
- costruzione della matrice degli errori.
- Determinazione dell’origine degli assi nel "piano delle fasi"
La posizione dell’origine degli assi del "piano delle fasi" viene determinata in modo da minimizzare il numero di "asole" con il metodo seguente:
- vengono determinate tutte le intersezioni delle "curve intrinseche" con l’asse orizzontale;
- viene valutato il punto intermedio tra essi, che ha la proprietà di massimizzare il numero di loop attorno all’origine;
- essendo le curve intrinseche simmetriche rispetto all’asse orizzontale, viene mantenuta tale coordinata come posizione verticale dell’origine degli assi.
- Riduzione delle "ambiguità"
Un metodo per rendere meno ambigua la corrispondenza tra i punti delle due scanline, consiste nello scomporle in tratti di minore lunghezza da trattare individualmente.
Per suddividere le scanline l’algoritmo fa riferimento alle "asole", cioè i loop che non hanno centro nell’origine del "piano delle fasi". Questi particolari loop rappresentavano un ostacolo per l’algoritmo descritto al paragrafo precedente e venivano eliminati.
Questi tratti di curva sono "poco" ambigui in quanto in numero generalmente ridotto e caratterizzabili da un numero elevato di parametri:
- posizione nel piano delle fasi (due coordinate);
- numero di tratti che le compongono;
- posizione nella sequenza, lungo la scanline.
che rendono l’algoritmo più robusto.
L’individuazione di un’"asola" avviene osservando l’evoluzione della fase. Quando si ha un’inversione del segno, cioè non appena il raggio vettore che segue la curva intrinseca cambia il senso di rotazione attorno all’origine, viene individuato il corrispondente punto che appartiene ad un’asola.
Per determinarne la coordinata iniziale del tratto di curva intrinseca che comprende l’asola, definita "nodo", che coincide con quella finale, è sufficiente determinare con un metodo esaustivo le intersezioni con i segmenti appartenenti alla curva in esame che precedono e seguono il punto di inversione della fase trovato, dal momento che, nella variante proposta, si opera considerando le "curve intrinseche" come spezzate anziché come curve interpolate.
Operando con le "asole", facciamo al tempo stesso un passo in avanti e uno indietro. Il passo in avanti è che dobbiamo stabilire corrispondenze tra asole invece che tra punti, e quindi abbiamo un numero di oggetti molto inferiore da considerare. Il passo indietro è che un'asola non occupa un punto del piano, ma una regione, e non c'è quindi una coppia di coordinate naturali per descrivere la posizione dell'asola, benché le coordinate del nodo siano un'approssimazione. Il grosso vantaggio è nella scomposizione della scanline in tratti più brevi che riduce il numero di match da considerare nella fase successiva dell’algoritmo.
- Matrice degli errori
Per determinare il match corretto vengono valutati gli errori commessi nell’associare un intero loop descritto da pixel appartenenti ad una scanline rispetto all’altra espressi in termini di distanze vettoriali.
Operando su un loop alla volta, viene valutata la distanza radiale tra i punti che presentano la stessa fase sulle due curve prendendo in considerazione, in sequenza, tutti i loop di una curva e confrontandoli con tutti quelli dell’altra.
Operando in coordinate polari si ha il vantaggio dell’immediatezza dei match, ma lo svantaggio che la fase è definita a meno di multipli dell’angolo giro.
Vengono inseriti i valori in una matrice degli errori E(l, r), commessi nell’associare tutti i loop relativi all’immagine destra rispetto a quella sinistra (o viceversa).
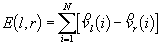
dove l e r sono i loop presi in esame e la differenza vettoriale  esprime la distanza tra punti ad uguale fase sulle curve sinistra e destra rispettivamente.
esprime la distanza tra punti ad uguale fase sulle curve sinistra e destra rispettivamente.
N = max(Nl, Nr)
con Nl e Nr pari al numero di punti appartenenti al loop l e r in esame.
La matrice ottenuta è triangolare per costruzione, in conseguenza della posizione relativa tra le immagini, per cui ha senso confrontare solo loop relativi a tratti di scanline oltre una pre-determinata posizione.
Nel caso di assenza di occlusioni, la matrice E é quadrata.
All’interno della matrice così costruita, viene determinata la sequenza di loop che dà il minimo errore. Anche in questo caso viene sfruttata l’informazione che i loop sono sequenziali per cercare, loop per loop, il match che dà il minimo errore.
Un’interpretazione grafica dell’algoritmo è la seguente. È possibile rappresentare come "immagine" la matrice degli errori, associando a ciascun elemento un pixel con un determinato valore della luminosità, secondo una scala di grigi ad esempio a 8 bit:
- il nero corrisponde allo zero;
- un pixel bianco corrisponde al valore massimo dell’errore, 255 nell’esempio;
- ai valori intermedi dell’errore viene associato un livello di grigio proporzionale all’interno della scala.
L’intero algoritmo si può interpretare come una trasformazione che associa alla coppia di immagini iniziali una nuova immagine che rappresenta gli errori nelle corrispondenze tra tratti di scanline (che formano i loop). Le corrispondenze ottimali sono determinate dalla diagonale principale dell’immagine più scura, in quanto i match corretti sono espressi dal minimo dell’errore.
- Prospettive
Il metodo indicato è caratterizzato da una codifica complessa attraverso l’uso delle cosiddette "curve intrinseche" rappresentate nel "piano delle fasi", e un match semplice e i punti dell’immagine vengono associati non in base alla loro posizione ma al loro aspetto. L’approccio rappresenta un’alternativa ai metodi tradizionali, in cui avviene l’inverso, e si presenta robusto, anche se oneroso dal punto di vista computazionale. La sperimentazione è tuttora in corso su casi più semplici in ambiente strutturato.
L’applicazione a più casi diversificati e di interesse pratico, le successive varianti e l’evoluzione della ricerca in questa direzione consentiranno di decretare sul metodo più appropriato e potranno dare ragione delle qualità dell’approccio descritto, che rappresenta indubbiamente una soluzione efficace per un problema ancora aperto: la stereopsi.
Al fine di migliorare le prestazioni del metodo, è possibile conseguire dei vantaggi nell’operare sull’intera immagine anziché sulla singola scanline. In tal caso, infatti, è possibile sfruttare le informazioni determinate nella scanline precedente, dato che le variazioni tra righe adiacenti sono minime. Questo consente di ridurre drasticamente le dimensioni delle routine
- nella determinazione delle asole;
- nella ricerca delle intersezioni per separare i loop;
- nel confronto tra i loop;
potendo operare limitatamente agli intorni dei punti già ricavati.
Un altro modo per migliorare l’efficienza dell’algoritmo consiste nel limitare il numero massimo di disparità d in base ad informazioni pregresse sulla scena osservata o tramite rilevazioni con un sensore di distanza.
Per velocizzare l’algoritmo è possibile implementarlo su hardware parallelo, assegnando l’elaborazione di ciascuna coppia di righe ad un processore diverso.
Una variante del metodo proposto, consiste nel considerare un "piano delle fasi" avente in ascissa e in ordinata la variabile luminosità e la sua derivata lungo l’asse immagine verticale, anziché quello orizzontale, come descritto in questo articolo. Naturalmente ciò comporterebbe la perdita delle proprietà fondamentali sulle corrispondenze tra loop lungo direzioni radiali per l’origine.
Analogamente possono essere immaginati "spazi" (¹
piani) delle fasi a più dimensioni, considerando sia gli integrali che le derivata successive. Probabilmente derivate di ordine superiore al secondo portano poca informazione perché fortemente condizionate dalla presenza del rumore.
- Conclusioni
In questo articolo sono stati proposti due algoritmi, di cui è stata verificata la fattibilità e di cui è in corso una campagna più estesa di prove al fine di estrinsecarne tutte le potenzialità e i limiti. Tali algoritmi rappresentano anche due esempi molto diversificati tra loro di approcci alla visione tridimensionale e hanno in comune numerosi campi di impiego.
Il primo è un algoritmo di tipo neurale basato sull’estrazione di feature geometriche tramite un sistema a singola telecamera e presenta i seguenti vantaggi:
- è general purpose in quanto può essere esteso ad altri tipi di primitive geometriche, diverse dalle ellissi;
- può essere applicato anche da personale non specializzato;
- permette una verifica dell’affidabilità, aspetto fondamentale nell’uso di reti neurali.
Il principale impiego consiste nella localizzazione di corpi contenenti parti circolari (ad esempio fori), comunemente presenti in campo industriale.
Il secondo algoritmo è un’evoluzione del metodo delle "curve intrinseche" per il problema della stereopsi. Con le varianti introdotte risulta di più semplice implementazione e più efficiente dal punto di vista computazionale, essendo passata da circa 30 a 3 s l’elaborazione di una scanline di 576 punti su workstation Indy - Silicon Graphics e circa 15 s su Pentium a 100 MHz.
- Ringraziamenti
L’autore tiene a esprimere la più profonda gratitudine al prof. Carlo Tomasi del Department of Computer Science dell’Università di Stanford (California) presso cui è stato sviluppato il metodo delle "curve intrinseche", per averlo accolto (con tuition fee a Suo carico) presso il Computer Vision Laboratory e per il proficuo lavoro svolto insieme.
Lo stage è stato finanziato con borsa di studio del Consiglio Nazionale delle Ricerche nell'ambito del "Programma di scambi internazionali per la mobilità, di breve durata, di studiosi/ricercatori di istituzioni di ricerca italiane e di studiosi stranieri (Anno 1995)".
- Bibliografia








