M. Lanzetta Institute of Mechanical Technology,

G. Tantussi University of Pisa, Italy

KEY WORDS: Stereo Vision, 3D Trajectory Reconstruction, Real-Time Tracking

ABSTRACT: Stereo Vision for assisted robot operations implies the use of special purpose techniques to increase precision. A simple algorithm in the reconstruction of 3D trajectories by real-time tracking is described here, which has been extensively tested with promising results. If the form of the trajectory is known a priori, the interpolation of multiple real-time acquisition yields an increase of precision of about 25% of the initial error, depending on the uncertainty in locating the points within the image. The experimental tests which have been performed concern the case of a straight trajectory.

STATE OF THE ART AND POSSIBLE APPLICATIONS

The importance of Artificial Vision for industrial applications is increasing even for small and medium enterprises for the reduction of hardware costs. It allows performing a closed loop process control not interfering with the observed system. Unfortunately this technology is limited by the low resolution of sensors; for this reason even a small increase in precision becomes attractive.

In this article a general algorithm for this purpose is described, which has been extensively tested at different space resolutions and camera configurations.

The main advantages of this algorithm are:

- easy to implement;

- fast;

- versatile.

The idea is to increase precision by multiple acquisitions, but not to interfere with the operations and in particular not to increase the acquisition time, the Observed Object (OO) is followed in real-time on its trajectory which precedes a critical point. This implies that a great computing power must be available, which is not a tight constraint when high accuracy is needed. The information to be exploited in the process concerns the kind of trajectory of the OO which is supposed to be known in parametric form. In common applications the presence of approximately straight lines is usual.

The Galilean relativity allows the application of this algorithm both to a moving camera (for instance in a robot hand-eye configuration [-] or ego-docking [] for autonomous robot or vehicle navigation [-]) and to a fixed camera observing a moving object. Some examples of the latter are:

• robot gripper obstacle avoidance [] or objects localisation and catching;
• in the case of autonomous navigation the so called echo-docking.

This algorithm can be applied both to trajectories in two and three dimensions.

Since in experimental tests it has been shown that it is resolution-independent, it can be applied in many different fields:

- mobile robot docking [] for the compensation of the errors due to incorrect positioning in the execution of a robot program relative to the robot base;

- closed loop control of assembly operations [-];

- tracking and control of an AGV position [];

- robot calibration, []; in the case of hand-eye configuration, Stereopsis can be achieved even with just one moving camera, by the observation of a known pattern [].

For all these cases it is necessary to know the OO trajectory in a parametric form.

SYSTEM CALIBRATION AND STEREOPSIS

To reconstruct the position of a point in 3D, more than one view is necessary or one view and at least one of the three coordinates.

In this article two cameras have been used with different configurations. The OO in the experiments was the sensor of a measuring machine. Since at any instant the OO coordinates are provided by a measuring machine, an absolute system has been defined coincident with its main axes. The transformation from three space coordinates to four image coordinates (a couple for each camera) is defined by the system calibration [].

This can be achieved by calibrating each camera separately through the minimisation of the squared errors of known 3D points projected onto the plane of view []. It sould be emphasised that the law of projection of a point with the pinhole camera model is non-linear. Expressing the problem in homogeneous coordinates we get the following expression

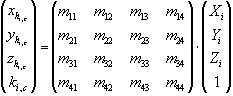(1)

where h_i stands for homogeneous coordinate of the i-th point of the c-th camera, with

; .

Eliminating k_i,c from the first two lines in equation (1) yields

(2)

The unknowns in this expression are the m_j,k , the elements of the matrix of projection of a point from 3D space onto the camera plane of view. To find an exact solution of the system almost six control points are needed. To get the maximum performances by a real system it is suitable to use a high number of points. Experimental tests have shown that about 30-40 points were enough for the utilised system.

Once the system has been calibrated, given a couple of point projections, it is possible to estimate the 3D coordinates calculating the pseudo inverse of the projection matrix. This latter is constituted of the calibration parameters taken from a couple of equations like the (2) for each camera c []. From equation (2) an expression in the form

(3)

can be derived. Equation (3) can be solved by the inversion of matrix A in the sense of least squared errors in order to find the unknown W vector.

It sould be noticed that the explained calibration model does consider translation, rotation, scale and perspective projection of a point in 3D space from/to one or more view planes, but it does not consider other effects which may introduce even a high degree of uncertainty, such as optical aberrations, lack of a suitable lighting and focus.

The application of this analytical model does not depend on the relative position between the camera and the observed system.

To achieve more general results, no further mathematical correction has been applied in experimental tests beside the Stereo Vision algorithm. In order to reduce the effect of optical aberration, the described algorithm has been applied with the fragmentation of the working space in smaller volumes and performing a different calibration on each of them.

Different configurations have been tested. The configuration which provides the lowest error (e. g. the Euclidean distance between the measured and the real point), was achieved when the three measured coordinates had the same accuracy. The best condition is with the camera optical axes perpendicular to each other.

In the case of two cameras forming an angle of about 75°, perpendicular to the Z axis and symmetrical with respect to the XZ plane, the accuracy on X coordinates were about half of the Y coordinates and about one third of the Z ones.

THE ALGORITHM

For the application of this algorithm, the following items are required:

• compensation of errors which can be approximated by a function of higher order than the calibration model or the trajectory form;
• knowledge about the real trajectory (e. g. if it is really a straight line or a curve);

otherwise the result of interpolation is to improve some trajectory parts and to worsen others.

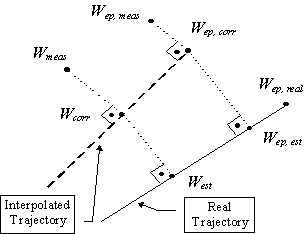
The algorithm can be summarised in the following steps:

1. Acquisition of the point coordinates in 2D
1. Interpolation for movement compensation
1. Recovery of the 3D point coordinates
1. Calculation of the interpolated trajectory
1. Correction of points

The chosen criterion to correct a measured point W_meas, is to project it perpendicularly onto the interpolated trajectory. The reason which inspired this idea is that the most accurate point belonging to the interpolated line is the closest one.

In order to treat fewer data, the real trajectory is described by its endpoints. Thus just two exact points are enough to test the algorithm on several measured points; this is very useful for practical applications.

For the algorithm estimation the following exact information is exploited:

• the known trajectory endpoints W_ep;
• for particular straight lines (parallel to the main axes), the two coordinates which remain constant during displacement.

For each measured point W_meas , an estimation of the exact one W_est , is obtained by projecting onto the known real trajectory the corresponding corrected point W_corr .

For the trajectory endpoints W_ep,meas whose corresponding real points W_ep,real are known, in experimental tests it has been shown that the distance between W_ep,est , the estimated one and the real endpoint W_ep,real is lower than 2/10 of initial error.

Considering the application of the described algorithm to a straight trajectory, the least squared errors straight line in parametric form, for any straight line non parallel to the main axes, is given by

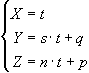(4)

with, for i ³ 2,

Given a measured point , the corrected point W_corr is found by substituting in equation (4)

EXPERIMENTAL DATA

The process performances, viz. the maximum space resolution and the OO maximum speed are limited respectively by the sensors resolution and by the computing power of the Artificial Vision system. The used system is made by a high performance acquisition and processing card. A complete frame with a resolution of 756x512 is acquired every 40 ms. One of the cameras sends a synchronisation signal to the other one and to the frame grabber that switches between them at the synchronisation frequency. This implies that to get the position of a point at instant j an interpolation of coordinates j-1 and j of the other camera is necessary. For this reason, after the acquisition of N couples of points, one gets M=2N-2 measured coordinates (the last one is static and the one before is taken during deceleration). The interpolation between point j-1 and j depends on the trajectory form, which is supposed to be known.

The A/D conversion and grabbing produce a negligible delay but does not affect the frequency of acquisitions of 25 non-interlaced frames/s.

The system is able to locate within a grayscale image of the indicated width and height, a pre-defined model in about 210 ms. This time can be reduced to about 1/10 by limiting the search area. In this specific application, the area reduction can be performed considering that in the time between two couples of acquisition, the OO moves just a few pixels from the present position along the pre-defined trajectory.

The system is able to locate within the image all the matches over a minimum score without increasing the search time. The option of following more than one point can be exploited

• to increase precision;
• to describe the trajectory of complex objects the central point of which is not visible or unknown;
• to retrieve the inclination of an object;
• to track multiple patterns for monocular robot hand-eye configurations [-].

In the next step the found coordinates of the OO in the image are used to calculate the corresponding 3D point performing the product of the pseudo inverse of matrix A and b in equation (3).

The Vision system has been programmed in order to follow the OO after it has entered the field of view at the beginning of its known trajectory and interrupts the acquisition when the OO stops. At this time the measured 3D trajectory has already been reconstructed and the corrected one is calculated. The parametric information on the corrected trajectory can now be used either to correct the end point or the whole sequence of points. The interpolated trajectory computation and the measured points correction are performed in less than 80 ms on a 120 MHz Pentium based PC.

In real-time tracking, line-jitter phenomenon can occur, viz. different lines in a frame are acquired with the OO at different positions. Line-jitter effect is to limit the OO speed relative to a camera because the OO model matching within the resulting image is affected by a greater error. Both the movement compensation and the correction through the described algorithm reduce the error of points belonging to a trajectory in space described at speeds up to about 40 mm/s. Below this value, the improvement coming from the application of this algorithm does not depend on the OO speed.

Different trajectories have been followed at different speeds in the range between 1 and 40 mm/s. For the same trajectory this implies acquiring an inversely proportional number of points in the following range: 150 ³ M ³ 10.

The estimation of the algorithm has been performed on the known final point of a sample of 26 straight trajectories inside a working space of about 300³ mm³.

1. An average reduction of 25% of the initial error the mean value of which is 1.13 mm, with a standard deviation of 0.47, has been achieved. This data consider the presence of less than 4% of negative values. The error was due to a bad approximation of the measured trajectory by a straight line; the other endpoint accuracy was improved.
1. For over 80% of these trajectories the error between the estimated and the real coordinates W_ep,est and W_ep,real (see figure) was lower than 20% of the initial error. As a consequence we can state that W_est represents a good estimation of the unknown real point corresponding to a measured one.

An extension of 1. to any measured point of the whole sequence is that by projecting it onto the interpolated trajectory we achieve a remarkable correction in most cases. In all tests, this has been shown by a reduction of standard deviation of about 50% on the examined sample.

A consequence of 2. is that projecting a corrected point onto the real trajectory, we can estimate its corresponding exact point coordinates.

Finally we can state that given a parametric description of a trajectory, we can estimate the errors on a sequence of measured points (the corresponding real point of which are unknown), their mean value, standard deviation, etc. by computing the distance between W_meas and W_est .

To get a higher precision, a higher space resolution (e. g. a higher camera resolution or a smaller workspace) is required and more sophisticated techniques of optical aberration compensation and a sub-pixel analysis are needed.

EXTENSIONS

In order to achieve a computation time reduction, this algorithm could be applied directly finding the interpolated trajectory as it will appear after projection on the camera sensors, e. g. if the trajectory is a straight line, finding the interpolated line inside the image, if the trajectory is a circular arc, finding the ellipse arc, etc. This sort of analysis would probably involve a different numerical approach to Stereo Vision, considering visual maps [], epipolar lines and other primitives [], and geometric relations between the absolute and the camera reference systems in order to optimise the overall process.

Dealing with a parametric description of primitives in space instead of points could allow providing a correction to the robot directly in this form.

Multiple Stereo algorithms [] are available to optimise the search in image; a direct use of features extracted from the image instead of operating on the coordinates could represent a shortcut.

In this article the least squared errors approach has been used; the experimental tests have been performed on a straight trajectory. A different kind of interpolation can be applied according to a different trajectory and error distribution (e. g. with low weights for less accurate points). Furthermore the benefits coming from the use of Kalman filter which is suitable for time dependent problems can be investigated.

CONCLUSIONS

A simple algorithm to increase accuracy in the case of an object moving on a trajectory the parametric description of which is known, has been described. The algorithm has been extensively tested on straight trajectories with different camera configurations. The interpolation of points both for movement compensation and for the trajectory calculation allow an increase of accuracy which depends on the initial error distribution.

It has been shown that a simple perpendicular projection onto the interpolated trajectory gives a suitable correction to most of the points of the whole sequence.

In order not to worsen some parts of the measured trajectory by the application of this algorithm, the following condition must be satisfied: absence of higher order discrepancies between

• the real trajectory and its mathematical parametric description;
• the real 3D points coordinates and the stereo reconstruction model.

Since the increased accuracy remains about the same on wide ranges of number of measured points, it has been shown that it is OO speed-independent.

If the OO inclination in the trajectory after the observed one is known, for instance in the case of the coupling of two parts, the angle between the interpolated trajectory and the exact one represents the correction to apply before the coupling.

The increase of accuracy can be exploited by increasing the field of view (thus compensating the reduction of spatial resolution) to monitor several critical points and trajectories with just one couple of cameras.

Once the interpolated trajectory is calculated, the absolute OO position can be reconstructed even after it exits one of the camera fields of view or if the localisation reliability of a camera has significantly decreased in that view area.

The method to test the described algorithm can also be used to test the performances of a general Artificial Vision system by employing just a few exact data (e. g. the trajectory endpoints).

REFERENCES